Coming to Statistica  
in 2022/2023

Zoom tutorials
using Explaineverything app
We a record sessions for you to listen to later

CALL STATISTICA NOW

Please contact Statistica
with questions or comments.
 © Copyright 2022  Statistica
 All rights reserved.

E-mail     anne@statistica.com.au

Phone           (08) 9457 2994

Place         Willetton, Western Australia

Twitter        @Anne_statistica

Mathematics & Statistic Tutor Perth - SPSS Help   

 Chi-Squared Test of Independence
SPSS output for Regression  Tests of Significance  
Normal distribution     SPSS Instructions   


Chi-Square Test of Independence 

Words to look  for          Related, Independence, Relationship, Depends, Expected

Layout to look for          Table with one variable across the top and one down the side.                                                                 

These will be the variables that replace the dots in the hypotheses

 Hypotheses

 Null Hypothesis:                 ............... and ............... are independent.
 Alternative Hypothesis     ............... and ............... are not independent.

Notice the first line has one word “ are ” and the second line has two words “ are not ”

The dots are replaced by whatever the variables are in the table i. e. the two variables which in the question.

         Test Data

Finding Expected values by using formula as well as subtraction. This formula calculates the Expected value if the two variables are indeed independent.

The formula is:

Expected Value = (Row Total)(Column Total)
                                           Grand Total

Subtraction will save some time but you may use the formula for all expected values. 
What do we mean by this?  The row and column totals of Observed and Expected values  are equal, so we can subtract to obtain other Expected values.

In the following tables, I have starred the values that you may calculate using the formula and the blank ones you would get by subtraction.

Ok, now put some numbers in so we can see how it works.

The Blue numbers are the row and column totals.
The Red numbers are the expected values obtained by Formula.
The Green numbers are the expected values obtained by subtraction.

 So 26 is obtained by     65 x 50
                                                            ¹²⁵

 So 18 is obtained by   65 -  (26 + 21)
 So  9  is obtained by   50 -  (26 + 15)

      Test Statistic

Evaluating the chi-square statistic,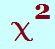

There is no short cut this time apart from a calculator but I still find it handy to write some values down. I tend to find it handy to write the values in the table format.
This saves time when you are checking as you can tell whether you got the same answer last time.  I have shown the the actual values below, but in the examination perhaps just the answers would do as long as you put the formula somewhere.

The Observed values are in Red.
The Expected values are in Blue

        = (O - E) ²      =     (26 -   20) ²  +  (15 -  17 )²  +  (9 - 13) ^{2
                              E                            20                     17                   13}

                      (21 - 23) ²   +  (10 - 13) ²   +  etc ...
                              ^{23                       13}

      P-value

The value is found in 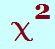tables
with degrees of freedom being (number of rows - 1) times (number of columns - 1)

When the level of significance is 0.05 then the following applies:

  If the p-value bigger  than 0.05   then  Do not reject the Null Hypothesis

  If the p-value smaller than 0.05 then  Reject the Null Hypothesis

 Decision and Conclusion.

If we Reject the Null Hypothesis,

then the results are statistically significant suggesting that there is sufficient evidence
to indicate that the two variables are not independent at the 5% significance level.

If we Do Not  Reject the Null Hypothesis,

then the results are not statistically significant suggesting that there is insufficient evidence
to indicate that the two variables are not independent at the 5% significance level.