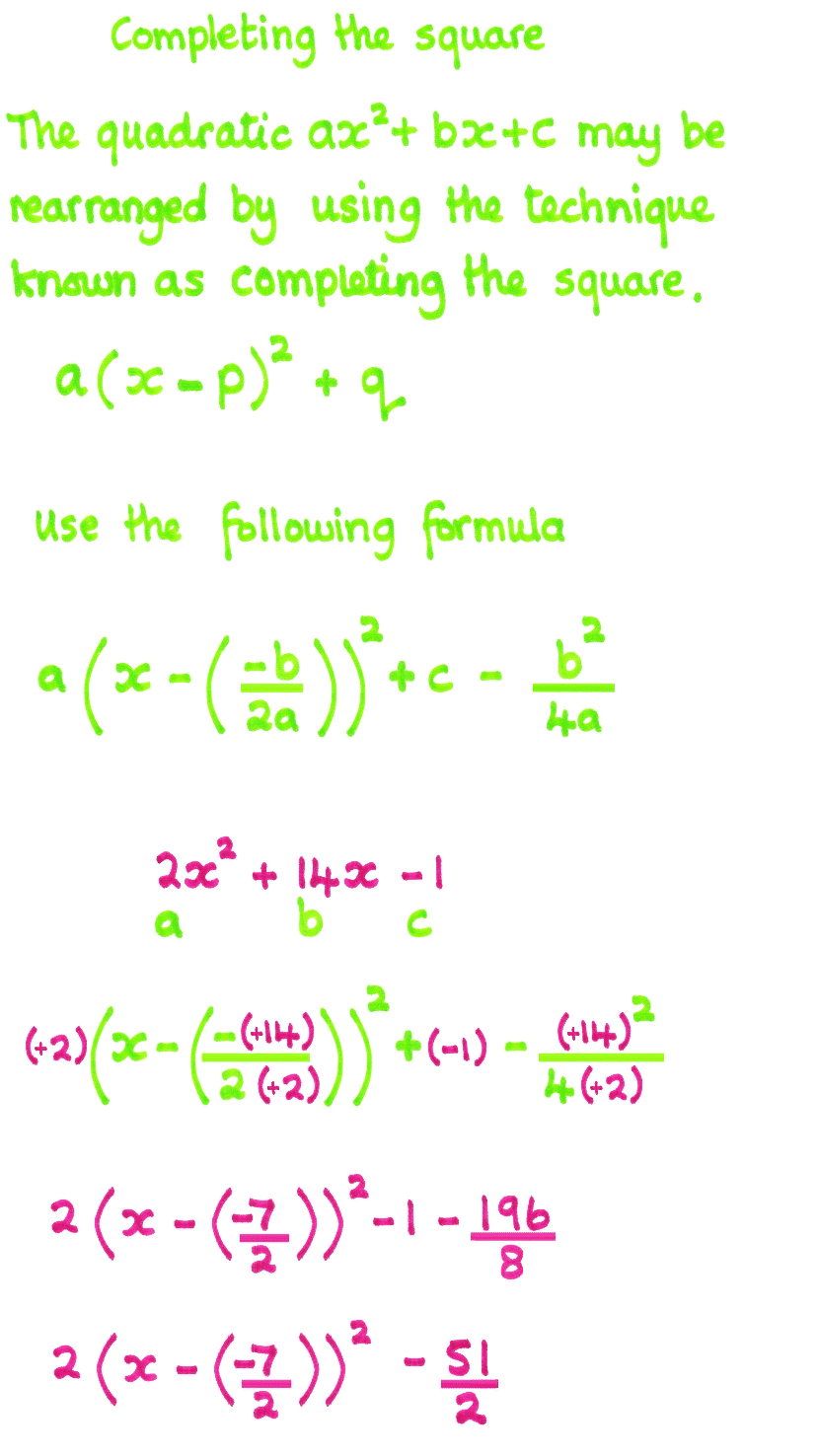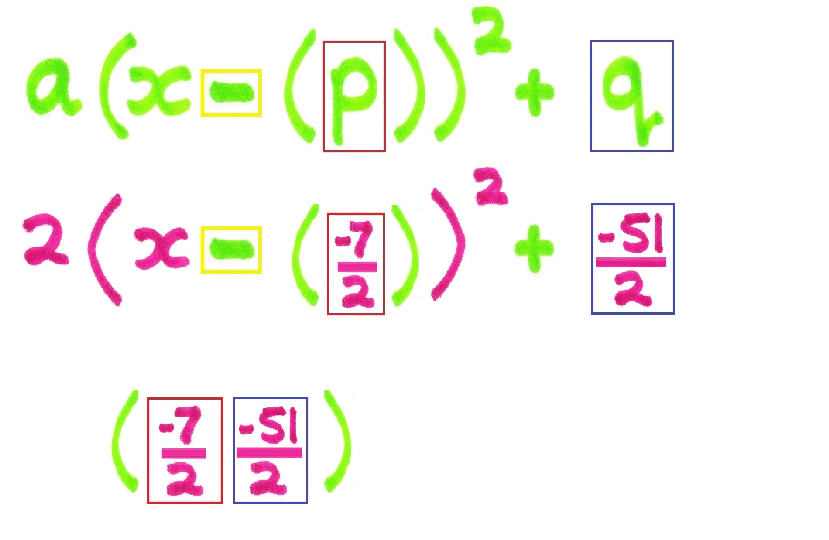Completing the Square
This is a technique that takes any quadratic expression rearranges to be a perfect square in doing so you will have subtract a portion. This portion is what you have added to make it a perfect square.
Examples of perfect squares
32
(x+1)2
(3x4 - 8)2
sin2 (x)
It is often known as the turning point form of a quadratic;
if the expression is written with a minus sign (in the yellow box) then
the value of p (in the red box) and
the value of q (in the blue box)
are the x and y coordinates of the turning point.
|